基础知识
- 原码、反码和补码是计算机存储数字的编码方式(表示方法)。
- ASCII码、utf-8和utf-16是计算机存储字符的编码方式。
你需要了解的存储单位
| 符号 | 中文 | 解释 |
|---|---|---|
| b (bit) | 比特,位 | 存放一位二进制数,即 0 或 1,最小的存储单位 |
| B (Byte) | 字节 | 1B = 8b |
| KB | KB | 1KB = 2^10B = 1024B |
| MB | 兆 | 1MB = 2^20B = 1024 * 1KB |
| GB | G | 1GB = 2^30B = 1024 * 1MB |
| TB | T | 1TB = 2^40B = 1024 * 1GB |
- 存储设备一般以B为常用单位;
- 宽带传输速度是以Kb为单位,与实际存储单位KB有所不同。(我办理了一个100M带宽,实际速度不会超过100/8=12.5M)
基本数据类型
| 类型 | 字节数 | 位数 | 最小 | 最大 |
|---|---|---|---|---|
| byte | 1Byte | 8Bit | -2^7(-128) | 2^8-1(127) |
| short | 2Byte | 2 * 8Bit | -2^15(-32768) | 2^15-1(32768) |
| int | 4Byte | 4* 8Bit | -2^31 | 2^31-1 |
| long | 8Byte | 8 * 8Bit | -2^63 | 2^63-1 |
| float | 4Byte | 4 * 8Bit | -2^ | |
| double | 8Byte | 8* 8Bit | ||
| char | 2Byte | 2* 8Bit | \u0000 | \uffff |
| boolean | 0 | 1bit | 0 | 1 |
浮点型
- float
- double
在数学中,特别是在计算机相关的数字(浮点数)问题的表述中,有一个基本表达法:
value of floating-point = significand x base ^ exponent , with sign
译为中文表达即为:
(浮点)数值 = 尾数 × 底数 ^ 指数,(附加正负号)
于是,float的指数范围为-127~128,而double的指数范围 为-1023~1024,并且指数位是按补码的形式来划分的。其中负指数决定了浮点数所能表达的绝对值最小的数;而正指数决定了浮点数所能表达的绝对值最大的数,也即决定了浮点数的取值范围。
1 | [高位] ------------------------> [低位] |
- 原码:符号位+数值的绝对值。
(1)以8位为例,1的原码为 0000 0001,-1的原码为 1000 0001。
(2)取值范围:11111111 ~ 01111111,即:-127 ~ 127。 - 反码:正数的反码是原码,负数的反码是在原码的基础上符号位不变,其他位取反的结果。
以8位为例:1的反码为 0000 0001,-1的反码为 1111 1110。 - 补码:正数的补码是原码,负数的补码是在原码的基础上符号位不变,其他位取反再加一,即:反码+1。
以8位为例:1的补码为 0000 0001,-1的补码为 1111 1111。 - 补码存在的意义
(1)1 - 1 = 1 + (-1) = (0000 0001)(原) + (1000 0001)(原) = (1000 0010)(原) = -2。错误
(2)3 + 5 = (0000 0011)(原) + (0000 0101)(原) = (0000 1000)(原) = 8。正确
(3)反码相减:3 - 4 = (0000 0011)(原) + (1000 0100)(原) = (0000 0011)(反) + (1111 1011)(反) = (1111 1110)(反) = (1000 0001)(原) = -1。正确
(4)反码相减:5 - 3 = (0000 0101)(原) + (1000 0011)(原) = (0000 0101)(反) + (1111 1100)(反) + 1(循环进位)= (0000 0010)(反) = (0000 0010)(原) = 2。正确
(5)1 - 1 = 1 + (-1) = (0000 0001)(反) + (1111 1110)(反) = (1111 1111)(反) = (1000 0000) = -0。
(6)1 - 1 = (0000 0001)(原) + (1000 0001)(原) = (0000 0001)(补) + (1111 1111)(补)= (0000 0000) (补) = (0000 0000) (原) = 0。
(7)-1-127 = (1000 0001)(原) + (1111 1111)(原) = (1111 1111)(补) + (1000 0001)(补) = (1000 0000)(补) = -128。
A、由(1)和(2)可知,原码相加是正确的,但是相减是错误的。
B、由(3)和(4)可知,反码相加减都是正确的。
C、但是由(5)可知,1-1的反码结果为-0,这个结果在数学上是没有意义的,为了解决这个问题,引入了补码。因为补码是在反码的基础上加1,故补码的加减是没有问题的,关键是1-1了。由(6)可知,补码完美的解决了1-1等于-0的尴尬局面,直接得到0。
D、由(7)可知,计算机底层算法规定了补码1000 0000 = -128。这也就导致了补码的取值范围由-127127变为-128127。
总结:
(1)由于原码相减结果不对,故使用了反码。但是反码1-1得到的结果是-0,这个在数学上是无意义的,为了导出1-1=0的正确结果,故使用了补码,同时规定补码1000 0000 = -128,从而可以将-0表示为-128,拓展了一个表示位,故8位二进制取值范围为-128~127。
(2)这里再次强调,在计算机中,数据都是以正数的补码的形式存在的。正数的补码是其本身,负数则是以其本身的正数的补码的形式存在的。
栗子:-123在计算机中的存储的值是1111 1011 -> 1000 0100 -> 1000 0101。
int
占用4个字节,即:32b,有符号位:从左数第一位。
取值范围:-2^31 ~ 2^31-1。
原因:0 代表 +0,-0 代表 -2^31,故负数比整数多一个。
数据以补码的形式存放在内存中。
对于+0和-0在内存中的存储方式。
1 | #include "stdafx.h" |
unsigned int
占用4个字节,即:32b,无符号位。
取值范围:0 ~ 2^32。
数据以补码的形式存放在内存中。
float
- 浮点数在计算机中用科学计数法表示,栗:1.0100011*2^7。
- 符号位:“+”或者“-”。
- 指数部分:2的幂指数,栗子中的“7”。
- 尾数部分:最高位为“1”的底数,栗子中的“10100011”。
- 栗子:15.987在计算机中存储方式。
1 | (1)15.987的整数部分原码:1111。 |
double
原理同上!
char
在内存中以ASCII码的形式存储。
栗子:
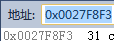
代码中字符是“1”,ASCII码为49,转换为16进制为31。
拓展
移位存储:
在存储浮点数时,若指数部分若不使用移位存储技术,则会导致0有两种表示方式:1000 000 0和0000 000 0。所以,为了最大化利用价值,同时保留正负性,在原数据的基础上加127,其结果如下:
1 | 0000 000 0 ~ 0111 111 1代表着 -127~0。 |
这样正负指数均可表示的数量保持一致。

