Hash,一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射pre-image)通过散列算法变换成固定长度的输出,该输出就是散列值。
HASH函数
哈希函数并不通用,比如在数据库中能够获得很好效果的哈希函数,用在密码学或错误校验方面就未必可行。在密码学领域有几个著名的哈希函数。这些哈希函数包括MD2\MD4\MD5,利用散列法将数字签名转换成的哈希值称为信息摘要,另外还有安全散列算法(SHA),这是一种标准算法,能够生成更大的(64bit)的信息摘要,有点类似MD4算法。
余数法
取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p,p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生碰撞。
折叠法
针对原始值是数字时使用,将原始值分为若干部分,然后将各部分叠加,得到的最后四位数字(或者取其他位数字都可以)来作为哈希值
基数转换法
原始值为数字时,可以将原始值的数制基数转为一个不同的数字。例如,可以将十进制的原始值转化为十六进制的哈希值。为了使哈希值长度相同,可以省略高位数字。
数据重排法
这个方法只是简单的将原始值中的数据打乱排序。比如可以将第三位到第六位的数字逆序排列,然后利用重排后的数字作为哈希值。
冲突及解决
不同的key值产生相同的地址,H(k1)=H(k2)
比如除留余数法:表长3时,3、6、9 会产生hash冲突
压缩存储一定会带来冲突。
开放寻址法
Hi=(H(key)+di) MOD m,i=1,2,3…,k(k<m-1),其中H(key)为散列函数,m为散列表长,di为增量序列,可有一下三种取法:
- di=1,2,3…,m-1,称线性探测再散列;
- di=12,22,32,…k2(k<=m/2),称二次探测再散列
- di=伪随机数序列,称为随机探测再散列。
再散列法
Hi=RHi(key),i=1,2,…,k RHi均是不同的散列函数,即在同义词产生地址冲突时计算另一个散列函数地址,直到冲突不再发生,这种方法不易产生”聚集“,但增加了计算时间。
链地址法(拉链法)
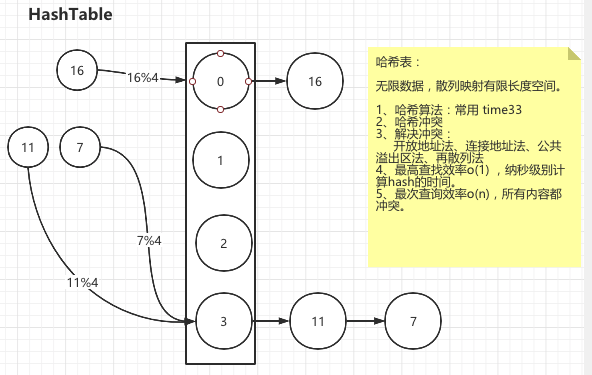
冲突的key,以链表存放在一个区域。查找时遍历节点的所有对象,也可以为这些对象构建索引加速查询。
建立一个公共溢出区
把冲突的key 都放到一个区域,查找时遍历这个区域所有数据即可。也可以创建所以加速查询。
查找性能
- 散列函数是否均匀
- 处理冲突的方法
- 散列表的装填因子
装填因子定义:α=填入表中的元素个数/散列表的长度
α是散列表装满程度的标志因子。由于表长是定值,α与”填入表中的元素个数“成正比,所以α越大,填入表中的元素较多,产生冲突的可能性就越大;α越小填入表中的元素较少产生冲突可能性越小。
![查找性能]()


