算法复杂度分析

为什么

跑一下代码，通过统计、监控就能得到算法执行的时间和内存占用情况，为何还需要做时间、空间复杂度分析呢？

这是事后统计法，这种方法有以下问题：32

依赖测试环境
比如程序可能在在i7cpu、与i9cpu下执行时间明显不同。
结果受到数据规模影响
对同一个排序算法、待排序数据有序度不一样，排序的执行时间就会有很大差别。

因此我们需要一个不用测试数据来测试，就可以粗略估计算法的执行效率的方法—时间、空间复杂度分析方法。

如何表示

大O表示法
假设 cpu处理一条指令的时间是一定的，每句代码粗略的等于一条指令的时间。那算法总时间就是,执行行数*每行执行时间。有以下几种情况：

程序执行行数与数据量n无关，时间复杂度为O(1)

int cal(int n){
	n+=1;
	return n;
}

程序执行行数与数据量n线下相关，时间复杂度O(n)

int cal(int n){
	int sum=0;
    for(int i=0;i<n;i++){
    	sum+=i;
    }
    return sum;
    
}

程序执行行数与数据量n指数相关，时间复杂度O(n^2)

int cal(int n){
	int sum=0;
    for(int i=0;i<n;i++){
    	for(int j=0;j<n;j++){
        	sum+=j;
        }
    }
    return sum;
}

大O时间复杂度表示法，并不能代表代码真正执行的时间，而是代码执行时间随着数据规模增长的变化趋势，所以，也叫做渐进时间复杂度简称时间复杂度。

时间复杂度分析

循环执行次数最多的一段代码

以下代码片段，只需要关心for循环里面的执行行数就行，时间复杂度即O(n)


int cal(int n) {
  int sum = 0;
  int i = 1;
  for (; i <= n; ++i) {
    sum = sum + i;
  }
  return sum;
}

加法原则

以下代码片段，总的时间复杂度就是量级最大的那段代码的时间复杂度。即O(n);

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   //时间复杂度 O（1）
   for (; p < 100; ++p) {
     sum_1 = sum_1 + p;
   }

   int sum_2 = 0;
   int q = 1;
   //时间复杂度O(n)
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }

   return sum_1 + sum_2 ;
 }

但以下时间复杂度为O(m+n),因为不知道谁大谁小，且都不是O(1)。

int cal(int n,int m) {
   int sum_1 = 0;
   int p = 1;
   //时间复杂度 O（m）
   for (; p < m; ++p) {
     sum_1 = sum_1 + p;
   }

   int sum_2 = 0;
   int q = 1;
   //时间复杂度O(n)
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }

   return sum_1 + sum_2 ;
 }

乘法原则

嵌套循环总的复杂度是各个片段复杂度的乘积。
以下代码片段时间复杂度为：O(m*n)，当m=n时，即O(n^2)

for(int i=0;i<n;i++){
	for(int j=0;j<m;j++){
    .....
    }

}

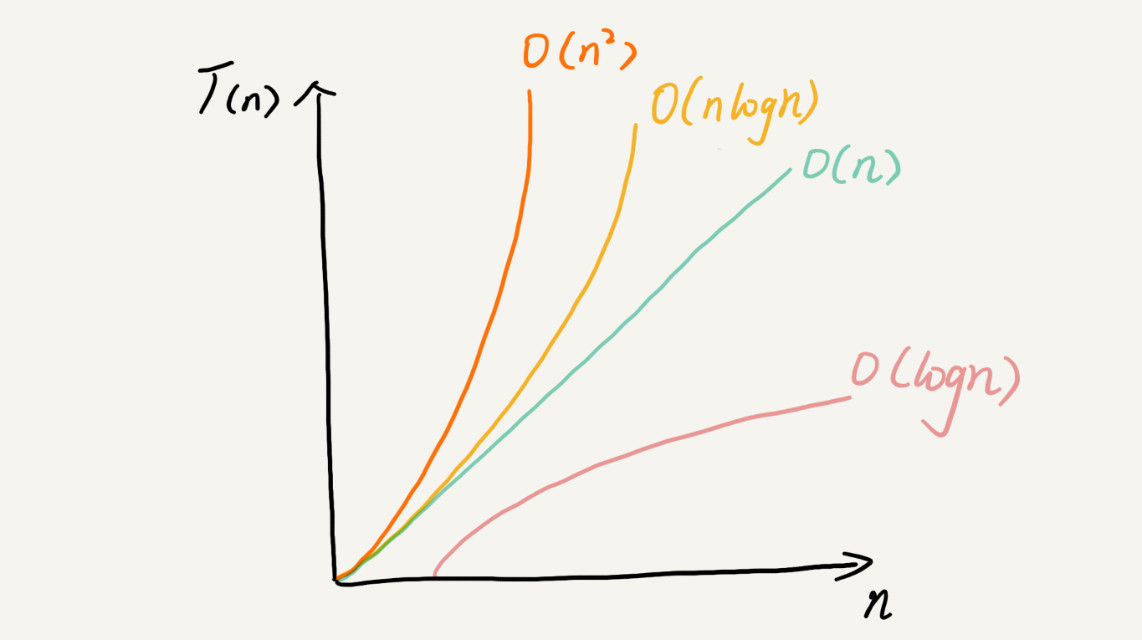
常见时间复杂度

常量阶 O(1)
线性阶 O(n)
对数阶 O(logn)
指数阶 O(2^n)
阶乘阶 O(n!)
线性对数阶 O(nlogn)
平方阶 O(n^{2)、立方O(n}3)…K次方O(n^k)

** 1、O(1) **
O(1)知识常量级时间复杂度的一种表示方法，并不是指只执行一行代码。
只要代码执行时间不随着n增大而增长，这样代码的时间复杂度就是O(1)。

只要算法中不存在：循环、递归、即便有上万行代码，其时间复杂度也是O(1).

** 2、O(logn)\O(nlogn)**
对数阶时间复杂度，例如：

i=1;
while(i<=n){
	i=i*2;
}

//i的取值
// 1、2、4、8、...
// 2^0,2^1,2^2，2^3、...
// 2^x=n,x=log2n

大O表示法是可以忽略系数的，所以下面代码时间复杂度也是：O(logn)

while(i<=n){
	i=i*3;
}

空间复杂度分析

空间复杂度全称渐进空间复杂度（asymptotic space complexity），标识算法的存储空间与数据规模之间的增长关系。
示例代码：

void print(int n) {
  //空间复杂度O(1)
  int a=100_000_000;
  
  //空间复杂度O(n)
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}