目录
- 树的定义
- 相关概念
- 树的分类
- 如何表示树
- 树的遍历
- 二叉查找树
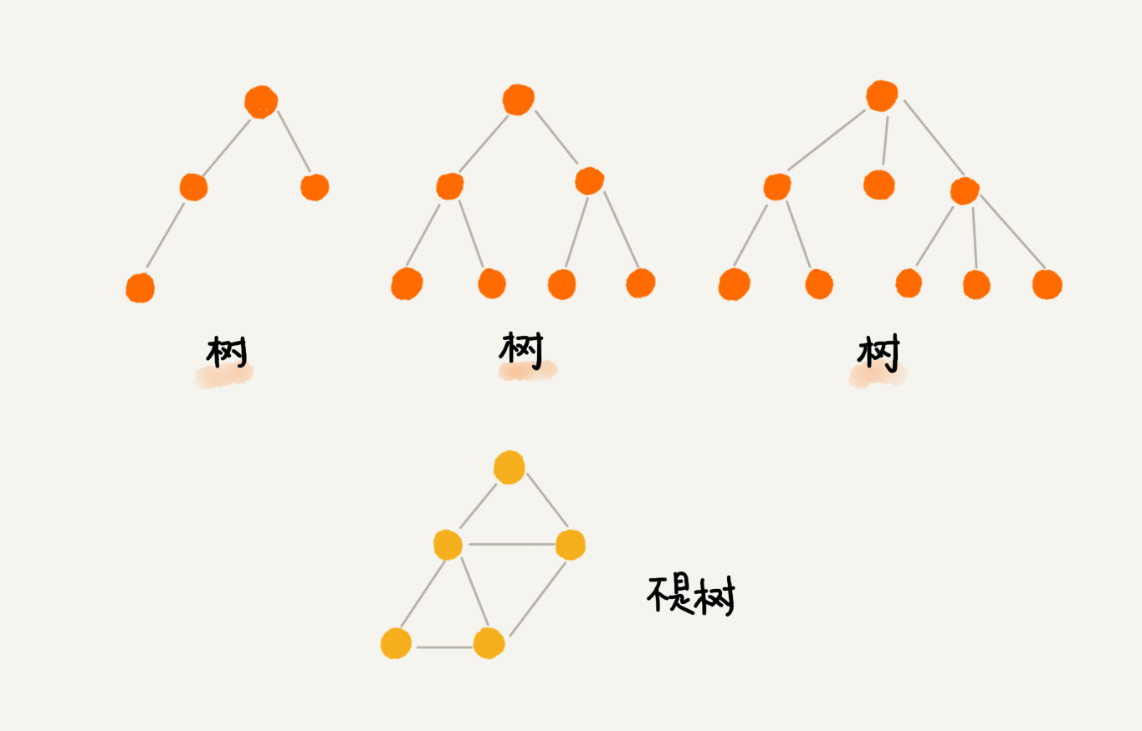
定义
![]()
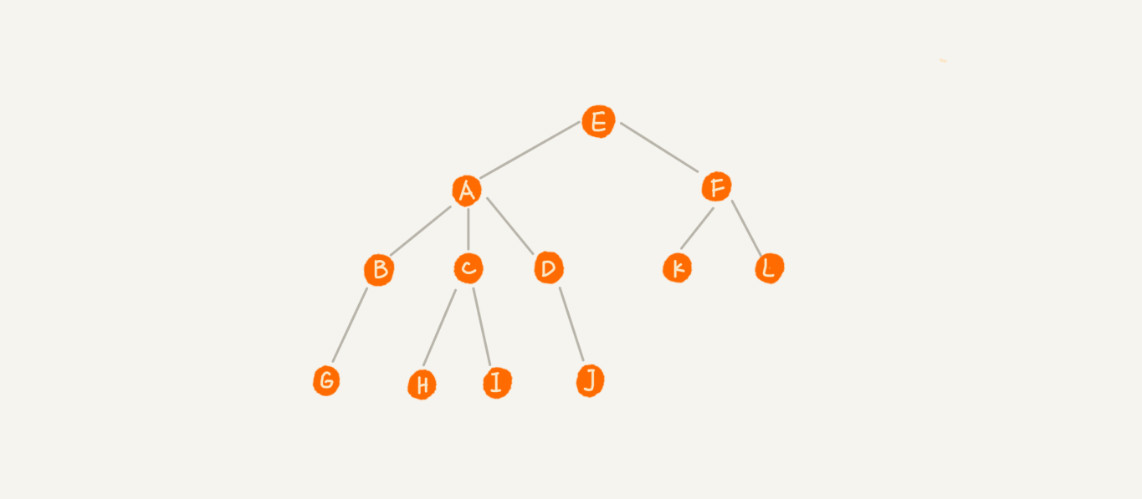
相关概念
![]()
- 根节点
E
- 父节点
E是A的父节点
- 子节点
A是E的子节点
- 兄弟节点
B\C\D互为兄弟节点
- 叶子节点
G\H\I\J\K\L 为叶子节点,他们没有子节点。
![]()
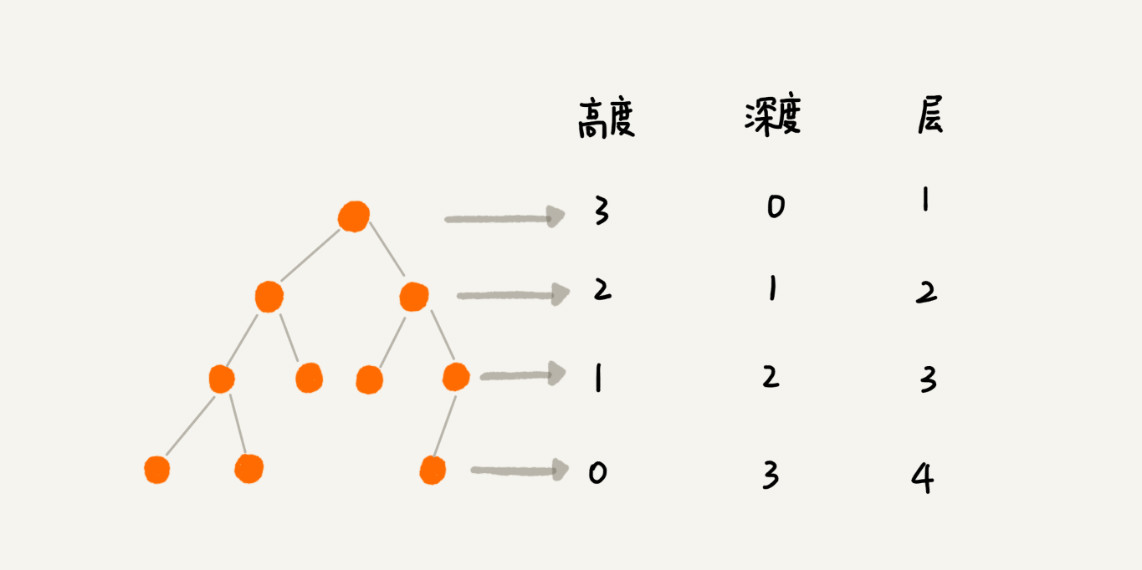
- 高度(Height),节点到叶子节点的最长路径(边数)。
- 深度(Depth),根节点到这个节点所经历的边的个数
- 层(Level),节点的深度+1
- 数的高度,根节点的高度
树的分类
二叉树
二叉树,每个节点最多有两个子节点,分别是左子节点和右子节点。
满二叉树
所有非叶子节点都有2个子节点的二叉树,是满二叉树。
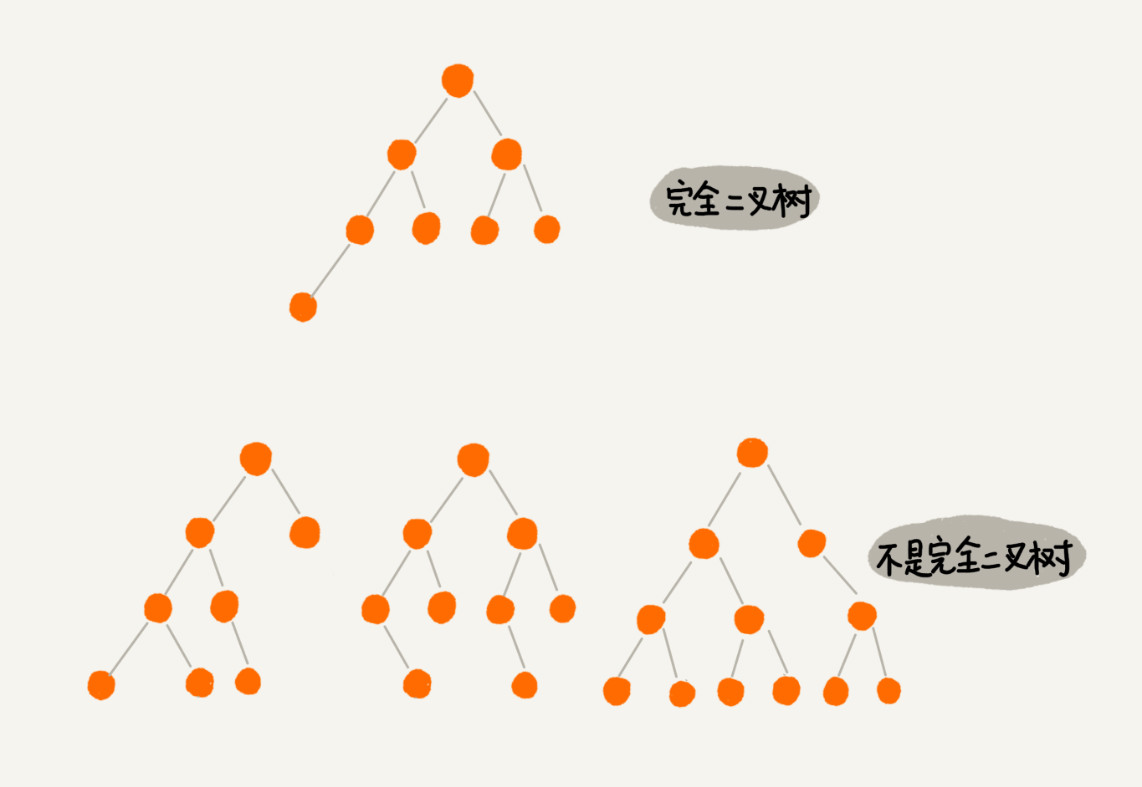
完全二叉树
除去最后一层其它层是满二叉树,最后一层从左到右无空节点。
![]()
表示一棵二叉树
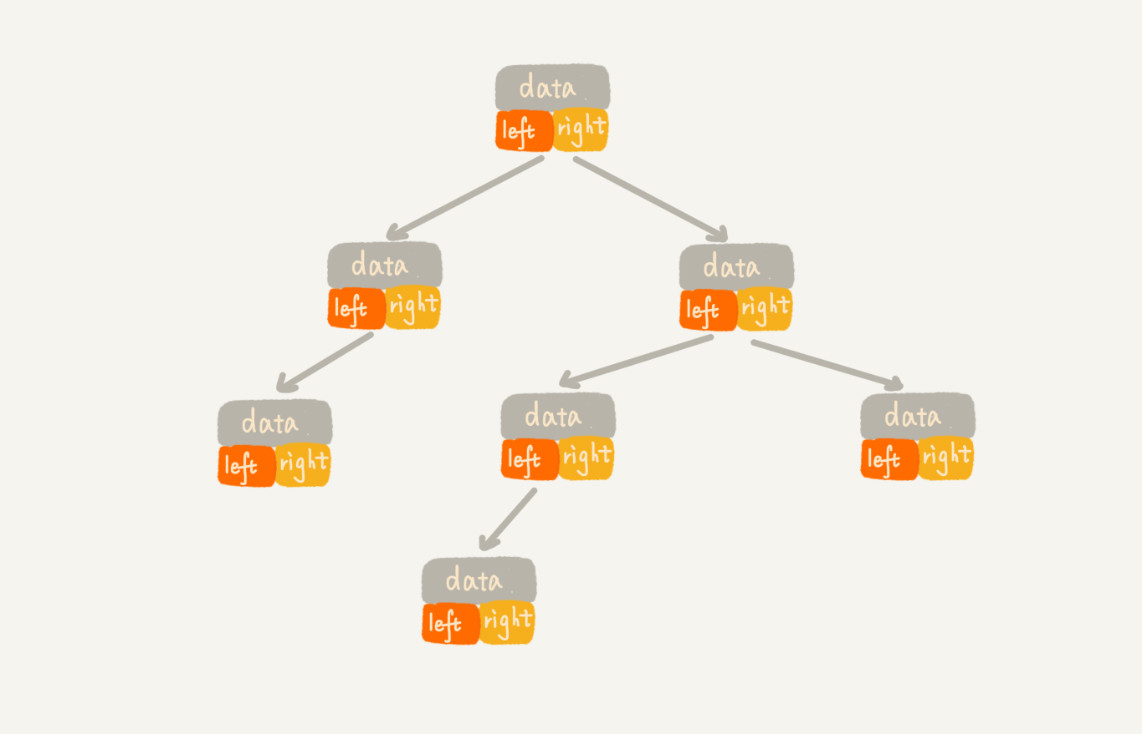
基于指针(引用)的链式存储法
- 每个节点包括数据、左子节点指针、右子节点指针
- 大部分采用此结构实现
- 简单、直观
![]()
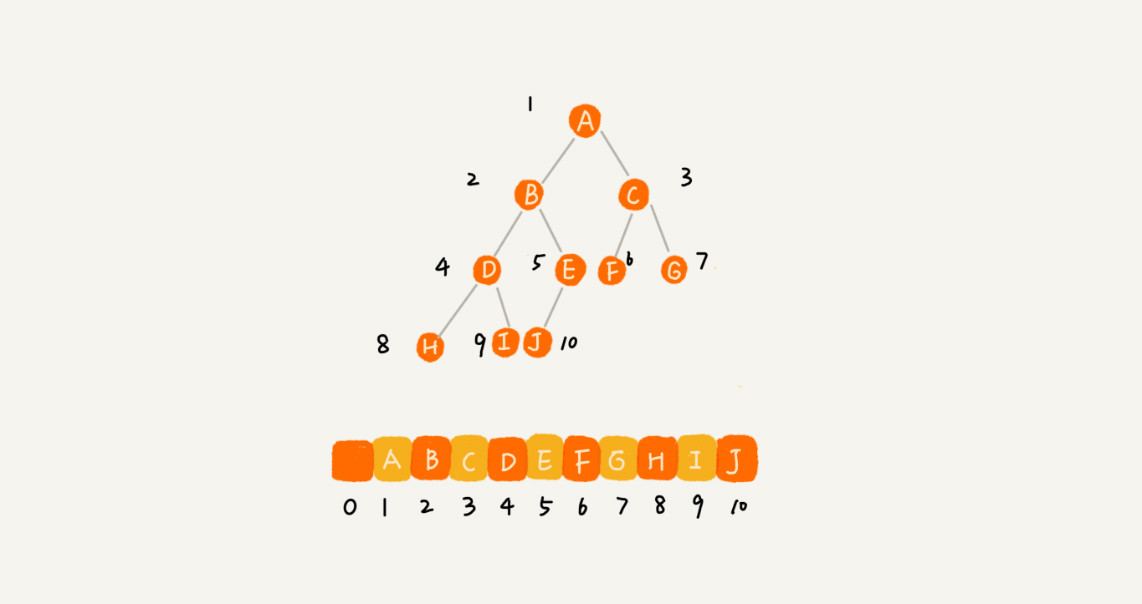
基于数组的顺序存储法
- 根节点i的左子节点在2i,右子节点在2i+1
- 即便没有那个节点位置也要空着
- 完全二叉树浪费一个存储位置(0)
- 非完全二叉树比较浪费空间
![]()
遍历二叉树
前序遍历
打印顺序:节点本身、左子树、右子树。
递归公式
1
2
3
4
5
6
| preOrder(r){
if(r==null)return ;
print r;
preOrder(r.left);
preOrder(r.right);
}
|
代码示例
1
2
3
4
5
6
| void preOrder(Node root){
if(root==null) reutrn ;
print root;
preOrder(root.left);
perOrder(root.right);
}
|
中序遍历
打印顺序:左子树–节点本身–右子树
递归公式
1
2
3
4
5
6
| inOrder(r){
if(r==null)return ;
inOrder(r.left);
print r;
inOrder(r.right);
}
|
代码示例
1
2
3
4
5
6
| void inOrder(Node root){
if(root==null) reutrn ;
inOrder(root.left);
print root;
inOrder(root.right);
}
|
后续遍历
打印顺序:左子树-右子树-节点本身
递归公式
1
2
3
4
5
6
| postOrder(r){
if(r==null)return ;
postOrder(r.left);
postOrder(r.right);
print r;
}
|
代码示例
1
2
3
4
5
6
| void postOrder(Node root){
if(r==null)return ;
postOrder(r.left);
postOrder(r.right);
print r;
}
|
二叉查找树
时间复杂度与树的高度成正比:O(height),O(logn)
二叉查找树需要满足 任意节点:
- 其左子树所有节点都要小于这个节点;
- 其右子树都要大于这个节点
查找
与当前节点比较:
- 小于当前节点,递归当前节点的左子树
- 大于当前节点,递归当前节点的右子树
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public class BinarySearchTree{
private Node tree;
public Node find(int data){
Node p=tree;
while(p!=null){
if(data>p.data){
p=p.right;
}else if(data<p.data){
p=p.left;
}else{
return p;
}
}
return null;
}
public static class Node{
private int data;
private Node left;
private Node right;
public Node(int data){
this.data=data;
}
}
}
|
插入
插入数据与当前节点比较:
- 大于当前节点,遍历其右子树,当右子树为空时插入其右子节点。
- 小于当前节点,遍历其左子树,当左子树为空时插入其左子节点
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public void insert(int data){
if(tree==null){
tree=new Node(data);
return ;
}
Node p=tree;
while(p!=null){
if(data>p.data){
if(p.right==null){
p.right=new Node(data);
return ;
}
p=p.right;
}else {
if(p.left==null){
p.left=new Node(data);
return ;
}
p=p.left;
}
}
}
|
删除
要删除的节点可能有0-2个子节点。
- 0个子节点,将它的父节点中引用置空
- 1个子节点,将子节点替换当前节点位置
- 2个子节点,将右子树中最小节点替换自己位置
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| public void delete(int data){
Node p=tree;
Node pp=null;
while(p!=null&&p.data!=data){
pp=p;
if(data>p.data){
p=p.right;
}else{
p=p.left;
}
}
if(p==null) return ;
//2个节点
if(p.left!=null &&p.right!=null){
Node minP=p.right;
Node minPP=p;
while(minP.left!=null){
minPP=minP;
minP=minP.left;
}
p.data=minP.data;//将minP的数据替换到p中
p=minP;//后面就是删除minP了
pp=minPP;
}
//删除节点是叶子节点或者仅有一个子节点
Node child;//p的子节点
if(p.left!=null){
child=p.left;
}else if(p.right!=null){
child=p.right;
}else {
child=null;
}
//删除的是根节点
if(pp==null){
tree=child;
}else if(pp.left==p){
pp.left=child;
}else{
pp.right=child;
}
}
|
删除操作可以通过标记删除,牺牲空间降低删除复杂度
支持重复值
- 方案一、节点采用集合数据结构、可以存放多个数据
- 方案二、按照大于处理
- 查找时,遇到相同值不能停止,继续查询右子树直到叶子节点
- 删除要依次删除每个节点
平衡二叉查找树
- 为了避免时间复杂度的退化
- 时间复杂度稳定在O(logn)