目录
堆是什么
- 堆是一个完全二叉树
- 堆中每个节点的值都必须≥(或≤)其子树的每个节点的值
如何实现一个堆
插入元素
- 将新元素放到数组最后的位置
- 堆化,插入新元素后的堆不一定满足堆的特性,堆化的过程就是让其重新满足堆的特性。
堆化方式:自下而上、自上而下,其逻辑相同:当前节点与其子节点(父节点)比较、交换。
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| /**大顶堆*/
public class Heap {
private int[] a; // 数组,从下标1开始存储数据
private int n; // 堆可以存储的最大数据个数
private int count; // 堆中已经存储的数据个数
public Heap(int capacity) {
a = new int[capacity + 1];
n = capacity;
count = 0;
}
public void insert(int data) {
if (count >= n) return; // 堆满了
a[count++] = data;
heapUp(count-1);
}
//自下向上堆化
public void heapUp(int i){
int p=i/2;//父节点
//退出递归条件
if(i<=0||a[i]<a[p]){return ;}
//事务
int tmp=a[i];
a[i]=a[p];
a[p]=TMP;
//递归
heapUp(i/2);
}
//自上而下堆化
public void heapDown(int i){
int left=i*2;
int right=i*2+1;
int maxPox=i;
if(left<count&&a[i]<a[left]){
maxPox=left;
}
if(right<count&&a[i]<a[right]){
maxPox=right;
}
//退出条件
if(maxPox==i){
return ;
}
swap(a,i,maxPox);
//递归
heapDown(maxPox);
}
}
|
删除堆顶元素
- 大顶堆,堆顶元素是最大值
- 小顶堆,堆顶原始是最小值
删除步骤
为何不直接将堆顶删除,然后向上移动节点?
堆的应用
堆的特性:
- 快速获得数组中的最大(最小)值。
- 快速获得数组中前n个最大值,后n个最小值。
堆的应用也正是利用了以上2个特性
堆排序
堆排序是一种选择排序算法,通过建堆找到数组中的最大(小)值,将其置换到数组末尾。调整数组长度为n-1,重复建堆、置换过程。
-
时间复杂度,O(nlogn)
-
空间复杂度O(1)
-
建堆
-
排序
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| //1.构建大顶堆
int len=arr.length;
for(int i=len/2;i>=1;i--){
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr,len,i);
}
//2.排序
for(int n=len-1;i>1;n--){
//堆顶、队尾置换
swap(arr,1,n);
//0,n-1,堆化
adjustHeap(arr,n,1)
}
/**
* 堆化
*/
public static void adjustHeap(int[] arr,int len,int i){
while(true){
int mx=i;
if(i*2<=len&&arr[i]<arr[i*2]){mx=i*2;}
if(i*2+1<=len&&arr[mx]<arr[i*2+1])mx=i*2+1;
if(mx==i)break;
swap(arr,i,mx);
i=mx;
}
}
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
|
优先队列
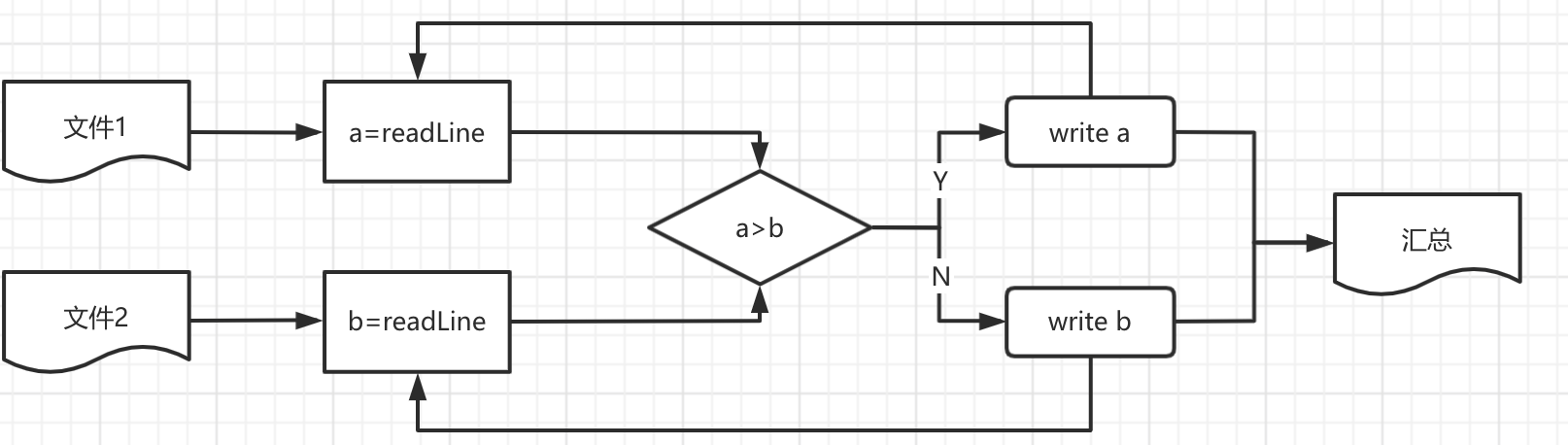
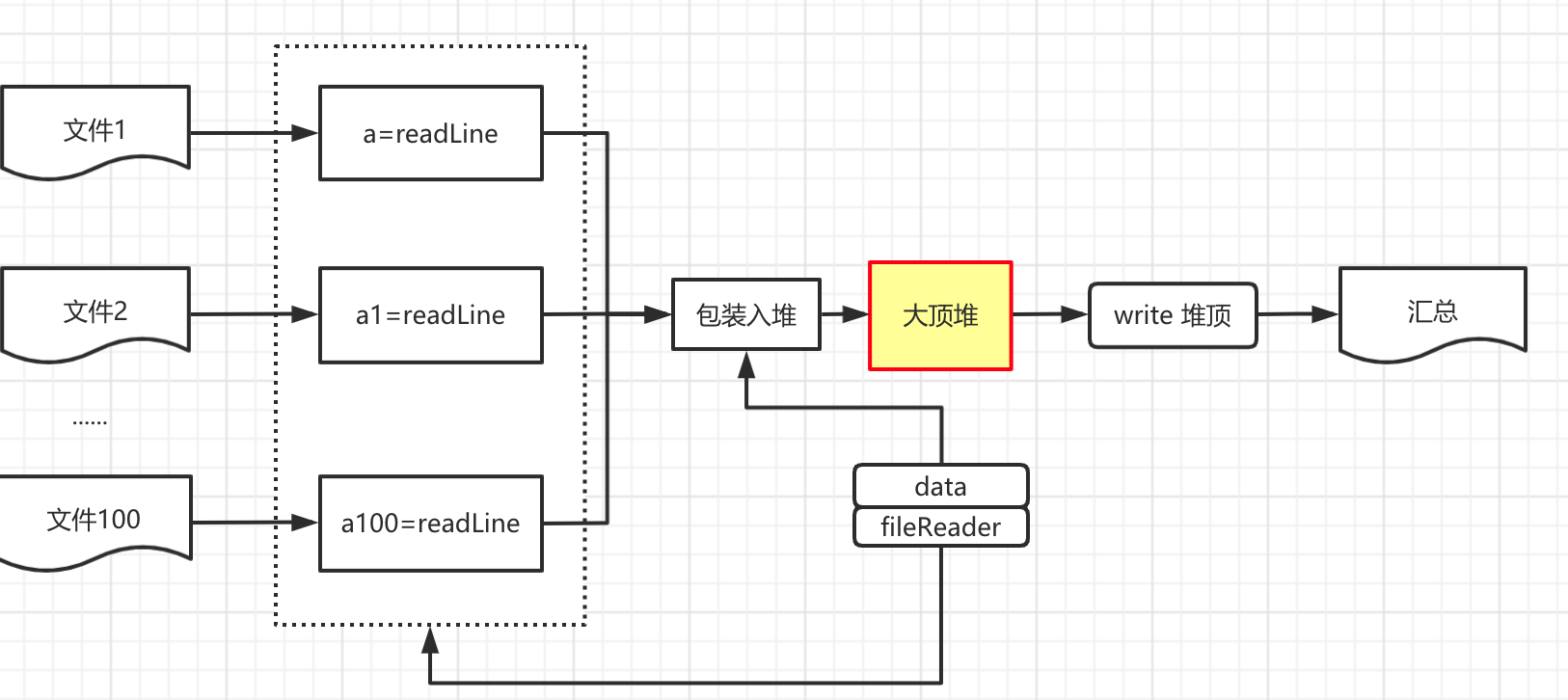
合并有序小文件
- 合并2个有序文件
![]()
- 合并100个有序文件
![]()
海量有序文件合并时,通过堆可以提升比较效率
高效定时器
- 普通方案:
每1秒遍历所有job的时间,查看是否需要执行;
- 堆优化
- 根据n秒后执行的n创建小顶堆
- 启动时查看小顶堆、堆顶的n,设置n-1秒后再查看
求中位数
中位数,就是处在中间位置的那个数。
- n=奇数,中位数=(n+1)/2
- n=偶数,中位数=(n/2+(n+1)/2)/2,中间两个数的平均数
静态数据
动态数据
无法完成排序再取值
建立一个小顶堆A和大顶堆B,各保存列表一半的元素,且规定:
- A保存 较大 一半,长度为N/2,或(N+1)/2.
- B保存较小的一半,长度为N/2,或(N-1)/2。
addNum(num)函数:
- 当m=n(N为偶数):需要向A添加一个元素。方法:将新元素num插入B,再讲B堆顶插入A;
- 当m≠n(N为奇数):需要向B插入一个元素。方法:将新元素num插入A,再将A的堆顶元素插入B;
- 时间复杂度:O(logN)
findMedian()函数:
- 当m=n,中位数=(A的堆顶+B的堆顶)/2
- 当m≠n,中位数=A的堆顶。
- 时间复杂度O(1)
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public class Median {
/***
* q1,大顶堆,存取较小的一半数据。
* q2,小顶堆,存储较大的一半数据。
*/
Queue<Integer> q1, q2;
public Median() {
this.q1 = new PriorityQueue<>();
this.q2 = new PriorityQueue<>((x, y) -> (y - x));
}
public void addNum(Integer num) {
if (q1.size() != q2.size()) {
q1.add(num);
q2.add(q1.poll());
} else {
q2.add(num);
q1.add(q2.poll());
}
}
public double findMedian() {
double result = (q1.size() != q2.size()) ? q1.peek() : (q1.peek() + q2.peek())*1.0 / 2;
return result;
}
}
|
topK问题
取集合中前k个值:
维护一个大小为K的小顶堆,依次将所有数据插入到小顶堆,当size大于k时移除堆顶。
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| //创建小顶堆
Queue<Integer> queue=new PriorityQueue();
//数据插入堆
for(Integer i:arrs){
queue.add(i);
if(queue.size()>k){
queue.poll();
}
}
//输出到数组
int[] result=new int[queue.size()];
int i=result.length-1;
while(!queue.isEmpty()){
result[i--]=queue.poll();
}
|
力扣习题
- 295,数据流的中位数
- 692,前K个高频单词
- 347,前k个高频元素
![]()
![]()